四轮全向轮的运动学模型 — 物理&数学模型的全面解算
越努力,越幸运,越拼搏,越自由
引言
在浙江省第八届&第九届机器人竞赛中,超市购物组机器人的底盘设计方向逐渐趋于全向轮的使用,在比赛中,几乎所有的队伍都已配置全向轮。但是,在网络检索四轮全向轮的运动模型解算结果中,很少有对四轮全向轮的物理模型进行解释,更多的是数学模型的公式推导。直接利用现有的成熟数学模型,固然可以成功实装全向轮运动,完成对小车的全向速度控制,但建立物理模型可以更大程度的理解全向轮运动。因此,本文根据自由度对全向轮小车车速进行矢量分解与叠加,从简单模型开始,巧妙的对全向轮小车物理模型进行分析,更具体地描绘了全向轮小车的运动,加深对全向轮模型的理解。
1.1 自由度定义
在求解四轮全向轮的运动学公式之前,我们需要明晰轮速与车速之间的关系:
1. 车速不等于轮速的矢量和
例如:汽车的四轮均以向前的 1m/s 速度转动,最终的车速为向前的 1m/s,而不是 1 * 4 = 4m/s ,此条不做过多赘述。
2. 在某一方向上,所有的主动自由度速度,都不会对小车的运动产生滑动摩擦,那么小车就会沿着此方向有一可叠加的矢量车速
车轮可以分为主动轮与从动轮,因此根据此定义,在本文模型中,将自由度分为主动自由度和被动自由度两种,并构建以下两个小车模型来阐述以上关系:
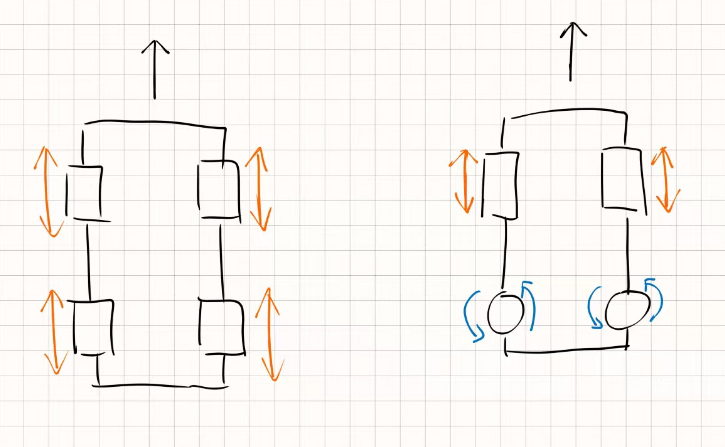
- 注:图中橙色表示主动自由度,蓝色表示被动自由度,下文同理
左图中,四个主动轮构成了四个方向相同的主动自由度,当四个主动轮都产生一个 V 的向前速度,那么小车也会向主动自由度的方向,以 V 速度向前行驶;当某一个主动轮的轮速增大为 2V 时,此时小车四个主动轮的速度不一致,就势必会产生滑动摩擦,应引入更复杂的模型进行解算。
右图中,小车前轮为两个主动轮,后轮为两个从动轮(万向轮)。当两个前轮都以 V 速度向前转动时,小车会沿着主动自由度方向,以 V 速度行驶;当右前轮速度增大至 2V 时,由于后轮为从动轮,不会对小车的运动产生滑动摩擦(滑动摩擦在运动时是必然存在的,此处讨论的是理论系统上,轮速不一致产生的滑动摩擦)。因此,小车依然会沿着主动自由度方向运动,由于前轮转速不一致,小车会逆时针旋转行驶,此时的主动自由度会随着车体旋转而旋转(因主动自由度方向与车轮方向一致),并始终与车速方向保持一致。
1.2 全向轮模型建立
全向轮的结构与模型的建立:
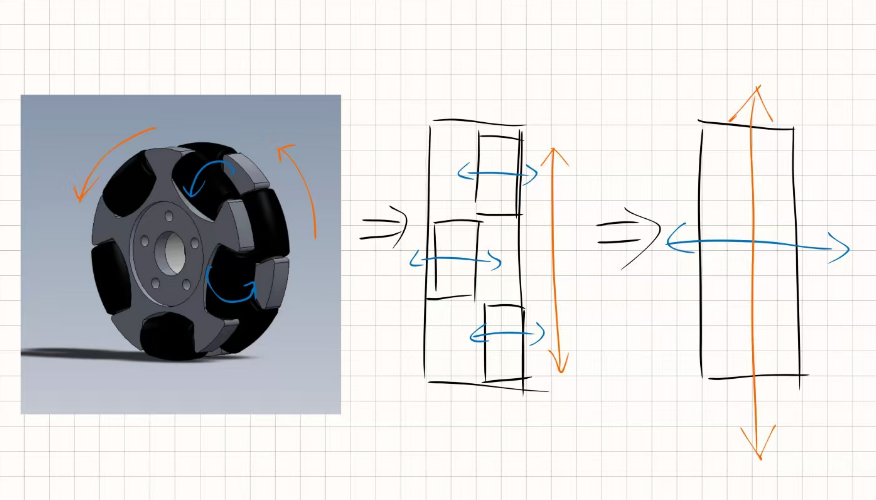
- 全向轮 3D 模型中主轴(电机)旋转的方向为主动自由度方向,滚子旋转的方向为被动自由度方向
- 各个滚子的被动自由度都与主动自由度空间垂直
- 简化得到全向轮模型,拥有一个主动自由度和一个被动自由度,两个互相垂直的自由度矢量叠加,即可得到任意方向的任意速度
1.3 四轮全向轮底盘物理模型建立
根据我们协会使用的四轮全向轮底盘结构,可以建立拥有四个主动自由度和四个被动自由度的物理模型。受到电路中叠加定理的启发,我将该四轮全向轮底盘模型分解为两个模型的叠加。
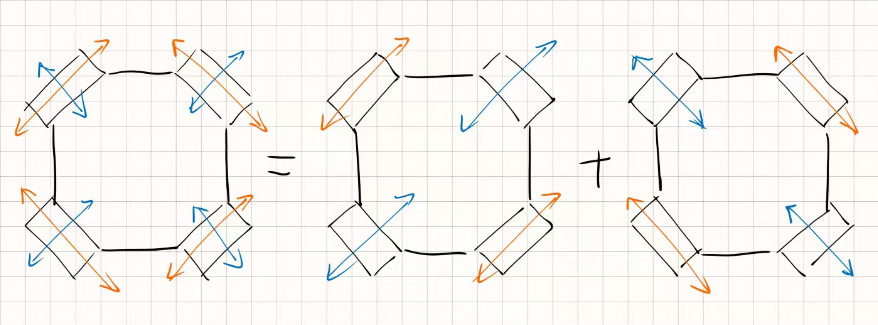
在两个模型中,各自的主动自由度和被动自由度方向一致,只要保证两个主动轮的轮速一致,就可以产生方向为主动自由度方向的相应车速。由于模型各自都没有因轮速不同产生滑动摩擦,并且两个模型产生的车速方向相互垂直,通过车速的矢量叠加,可以得到该全向轮底盘的最终车速。
1.4 四轮全向轮底盘数学模型建立
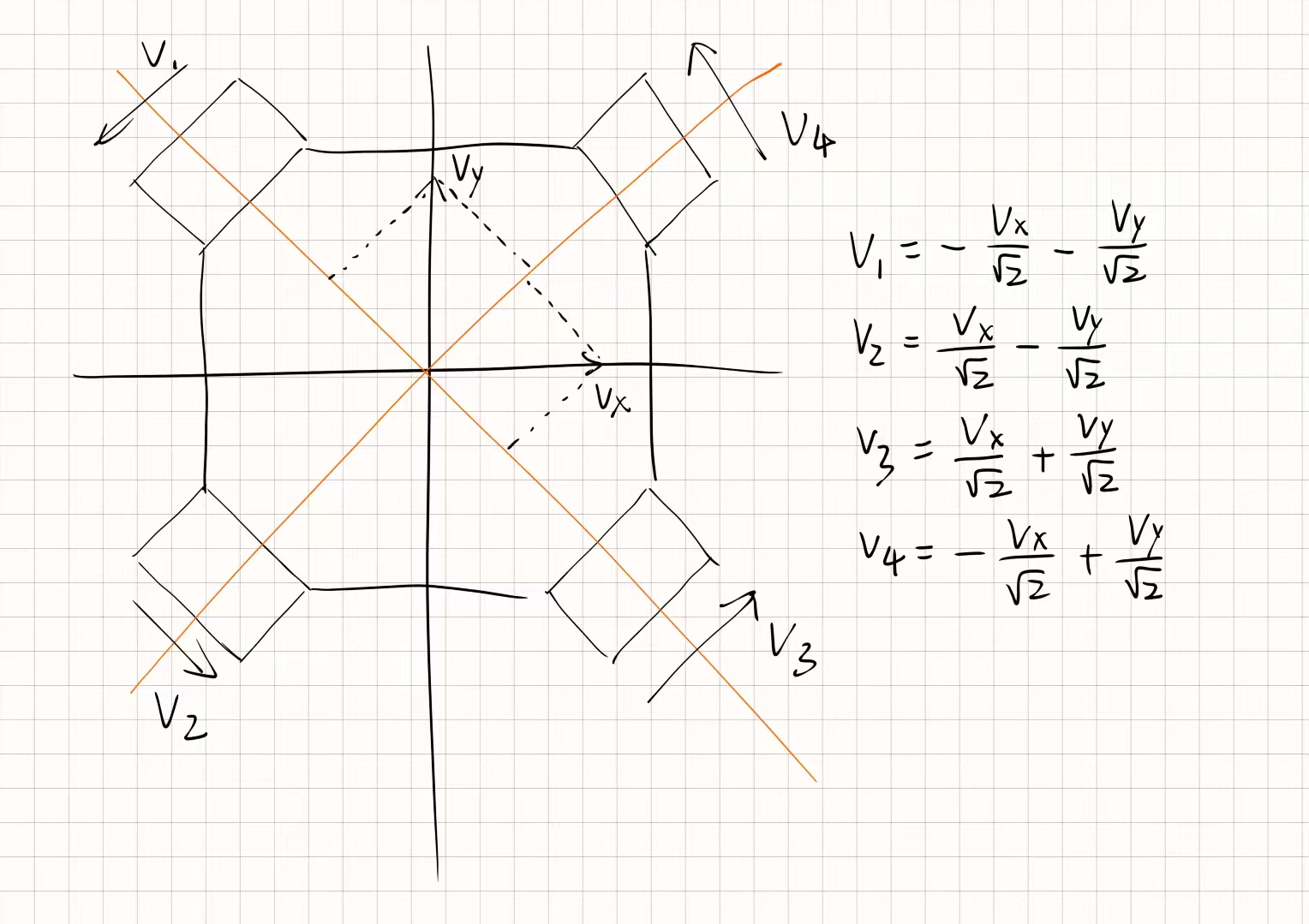
- 实际搭建的全向轮底盘,其四个电机的转速正方向应以逆时针或顺时针规则分布。由此,我们对四个轮子的正方向进行逆时针定义,如上图箭头所示
- 虽然直接将机器人坐标系(速度坐标系)定义在主动自由度方向上会简化计算,但由于实际使用中,横轴与纵轴的定义更符合常理,也更利于移植与扩展。因此,对速度在横轴与纵轴上做分解,以 X 轴正方向为正,Y 轴正方向为正,分为 Vx 和 Vy
- 最后,只需将 Vx 和 Vy 再次分解到机器人的两个主动自由度上,通过同一自由度上的两个速度叠加,即可得到四个轮子的最终转速。
ps:在得出的公式后都加上 wL ,即可让底盘解算具有自转功能
1.5 参考程序
当全局坐标系与机器人坐标系重合时,代码如下:
void chassis_move(float target_speed, float target_theta, float target_omega) {
//target_speed 速度大小;target_theta 速度方向;target_omega 自转速度
chassis.Radius = 300; //底盘半径
float speed[4]; //速度计算值
float speed_X = target_speed * cos(target_theta); //全局坐标系下的x轴速度
float speed_Y = target_speed * sin(target_theta); //全局坐标系下的y轴速度
speed[0] = ( - speed_X - speed_Y + chassis.Radius * target_omega) / sqrt(2);
speed[1] = ( speed_X - speed_Y + chassis.Radius * target_omega) / sqrt(2);
speed[2] = ( speed_X + speed_Y + chassis.Radius * target_omega) / sqrt(2);
speed[3] = ( - speed_X + speed_Y + chassis.Radius * target_omega) / sqrt(2);
for (int i = 0; i < 4; i++){
MotorController_SetSpeed(i+1,(int)speed[i]);
}
}1.6 番外...
写博客累累的捏......😣我看谁不一键三连😡😡😡
留言